Dạng toán tương giao vật thị hàm số là dạng toán vô cùng rất gần gũi đối với các bạn học sinh. Dạng toán này lộ diện thường xuyên trong số bài thi quang quẻ trọng. Vị vậy chúng ta hãy nuốm chắc triết lý và biết phương pháp giải bài xích tập của dạng toán này để được điểm tối đa trong những bài kiểm tra. Sau đây hãy cùng CMath khám phá và ôn tập về sự tương giao của vật thị hàm số nhé.
Bạn đang xem: Phương pháp đồ thị trong toán học
Lý thuyết sự tương giao thứ thị hàm số
Giao điểm của trang bị thị hàm số y = f(x) với y = g(x) bao gồm tọa độ là nghiệm của hệ phương trình y = f(x) cùng y = g(x).
Phương trình hoành độ giao điểm: cho f(x) = g(x) (1)
Tương giao thiết bị thị hàm số chính là số giao điểm của 2 đồ gia dụng thị bởi nghiệm của phương trình (1).
Tương giao trang bị thị hàm số phân thức bậc nhất (C): y = (ax + b)/(cx + d) và đường thẳng d: y = kx + m.
Ta tất cả phương trình hoành độ giao điểm như sau:
(ax + b)/(cx + d) = kx + m ⇔ Ax^2 + Bx + c = 0 (1)
Đường thẳng d: y = kx + m cắt (C): y = (ax + b)/(cx + d) tại 2 điểm rành mạch ⇔ (1) gồm 2 nghiệm minh bạch khác –d/c.
Lúc này ta thấy hoành độ giao điểm của phương trình giao điểm thỏa mãn nhu cầu hệ thức Viet của phương trình (1).
Tương giao đồ vật thị hàm số phân thức bậc bố (C): y = ax^3 + bx^2 + cx + d và con đường thẳng d: kx + m
Ta có phương trình hoành độ giao điểm như sau: ax^3 + bx^2 + cx + d = kx + m (1)
Ta nhẩm nghiệm x = x0 rồi mang lại phương trình với dạng (x – x0)(Ax^2 + Bx + c) = 0 ⇔ x = x0 hoặc Ax^2 + Bx + c = 0 (2)
Đường trực tiếp d cùng đồ thị hàm số (C) cắt nhau trên 3 điểm riêng biệt ⇔ (2) tất cả 2 nghiệm minh bạch khác với x0.
Ví dụ vào trường hợp A(x0; kx0 + m); B(x1; kx1 + m); C(x2; kx2 + m) Là tọa độ của 3 nút giao nhau giữa con đường thẳng d với đồ thị (C).
Khi kia nghiệm x1; x2 sẽ thỏa mãn nhu cầu định lý Viet: x1 + x2 = –B/A cùng x1.x2 = C/A
Tương giao vật thị hàm số phân thức bậc bốn trùng phương (C): y = ax^4 + bx^2 + c và mặt đường thẳng d: y = m
Ta bao gồm phương trình hoành độ giao điểm như sau: ax^4 + bx^2 + c = m (1)
Ta để t = x^2 (t 0), tiếp đến đưa phương trình (1) về dưới dạng at^2 + bt + c – m = 0 (2)
Bài tập vận dụng
Dạng 1: Tìm nút giao nhau giữa 2 vật thị hàm số.
Lý thuyếtHàm số y = f(x) có đồ thị (C1), hàm số y = g(x) tất cả đồ thị (C2). Chúng ta thực hiện quá trình sau phía trên để kiếm tìm giao điểm của 2 đồ gia dụng thị hàm số:
Bước 1: Lập phương trình hoành độ giao điểm của hàm số f(x) = g(x).Bước 2: Giải phương trình hoành độ giao điểm và tìm được x, từ đó suy ra y và suy ra điểm giao của 2 thiết bị thị.Bài tậpBài tập 1: tìm giao điểm của vật thị (C): y = x^3 – 3x^2 + 2x + 1 và d: y = 1
0123Hướng dẫn giải:
Lập phương trình hoành độ giao điểm, ta được: x^3 – 3x^2 + 2x + 1 = 1 ⇔ x^3 – 3x^2 + 2x = 0 ⇔ x=0; x = 2 hoặc x = 2.
Suy ra có 3 giao điểm → chọn câu trả lời D.
Bài tập 2: Ta gọi giao điểm của trục hoành cùng đồ thị (C): y = x^4 + 2x^2 +3 là A(x1;y1), B(x2;y2). Tính tổng x1 + x2?
0124Hướng dẫn giải:
Lập phương trình hoành độ giao điểm, ta được: x^4 + 2x^2 +3 = 0 ⇔ x^2 = 1 hoặc x^2 = –3 → x = 1 hoặc x = –1.
Suy ra tất cả 2 giao điểm A(–1;0) cùng B(1;0) → x1 + x2 = 0 → chọn câu trả lời A.
Bìa tập 3: tìm giao điểm của hàm số (C): y = (x^2 – 2x – 3)/(x – 1) và mặt đường thẳng y = x+ 1.
(–1;0)(2;3)(1;2)(4;5)Hướng dẫn giải:
Lập phương trình hoành độ giao điểm để tìm tương giao đồ thị hàm số, ta được: (x^2 – 2x – 3)/(x – 1) = x + 1 (điều kiện x không giống –1).
Xem thêm: Nhà hàng gần pandora trường chinh có gì ăn, nhà hàng gần pandora city shopping mall
→ x^2 – 2x – 3 = (x + 1)(x – 1)
⇔ x^2 – 2x – 3 = x^2 –1
⇔ –2x = 2 → x = 1 → y = 0
Chọn đáp án A.
Dạng 2: Biện luận theo tham số m.
Lý thuyếtCác bước tiến hành tương giao vật thị hàm số theo cách thức cô lập thông số m:
Bước 1: Lập một phương trình hoành độ giao điểm gồm dạng F(x;m) = 0Bước 2: cô lập tham số m rồi đem đến f(m) = g(x)Bước 3: Lập bảng biến chuyển thiên đối với hàm y = g(x)Bước 4: dựa vào bảng biến chuyển thiên với yêu mong của đề bài để suy ra các giá trị của m thỏa mãn.Phương pháp xa lánh tham số m sử dụng các tính chất đặc trưng của phương trình tương giao thiết bị thị hàm số.
Phương trình bậc 2 ax^2 + bx + c = 0Phương trình trên có 2 nghiệm tách biệt nếu > 0Phương trình trên có 1 nghiệm khi = 0Phương trình trên vô nghiệm lúc Phương trình bậc 3 ax^3 + bx^2 + cx + d = 0Nếu đoán được nghiệm x = x0 của phương trình tương giao đồ dùng thị hàm số ta có thể dùng phép phân chia đa thức hoặc sơ thứ Horner để phân tích thành nhân tử.Khi đó: ax^3 + bx^2 + cx + d = 0 ⇔ x = x0 hoặc ax^2 + b’x + c’ = 0 (*)
Dựa vào yêu mong đề bài, giải phương trình (*).
Nếu ko nhẩm được nghiệm hoặc không xa lánh được thông số m thì bài toán giải quyết và xử lý theo phương pháp dùng rất trị của hàm số.Phương trình trùng phương bao gồm dạng như sau: ax^4 + bx^2 + c = 0Đặt t = x^2 (điều kiện t 0), phương trình ⇔ at^2 + bt + c = 0 (2)Để phương trình gồm đúng 1 nghiệm thì (2) có 2 nghiệm thỏa mãn t1 Để phương trình bao gồm 2 nghiệm thì (2) có nghiệm nghiệm thỏa mãn t1 Để phương trình có 3 nghiệm thì (2) có 2 nghiệm vừa lòng 0 = t1 Để phương trình gồm 4 nghiệm thì (2) tất cả 2 nghiệm thỏa mãn nhu cầu 0 Bài tậpCho hàm số sau: y = 2x^3 – 3mx^2 + (m – 1)x +1 gồm đồ thị là (C). Tìm tham số m thế nào cho d: y = –x + 1 cắt (C) tại 3 điểm phân biệt.
(–;0) (8/9;)(–;–8/9) (0;)(0;8/9)(–8/9;0)Hướng dẫn giải:

Dạng 3: tìm kiếm tham số m nhằm giao điểm thỏa mãn nhu cầu điều kiện mang đến trước.
Lý thuyếtCó vật thị của 2 hàm số là y = f(x) và y = g(x)
Ta có phương trình hoành độ giao điểm tương giao trang bị thị hàm số là f(x) = g(x)


Cho hàm số sau: y = x^4 – (3m +2)x^2 + 3m tất cả đồ thị (C). Kiếm tìm tham số m nhằm d: y = –1 cắt (C) trên 4 điểm tất cả hoành độ nhỏ dại hơn 2.
m không giống 0–⅓ –2 A cùng B đúngHướng dẫn giải:

Dạng 4: Biện luận theo m số giao điểm của 2 vật thị phụ thuộc bảng trở nên thiên và đồ thị hàm số.
Lý thuyếtTương giao đồ gia dụng thị hàm số 2 hàm số (C1) với (C2) có đồ thị theo thứ tự là y = f(x) và y = g (x). Giao điểm của 2 vật thị là nghiệm của phương trình f(x) = g (x).Y = m là con đường thẳng qua điểm M(0;m) và tuy nhiên song với Ox. Nhìn vào bảng biến hóa thiên tương giao đồ vật thị hàm số ta phát hiện số giao điểm của mặt đường thẳng y = m và đồ thị (C).Bài tậpCho hàm số y = f(x) được xác minh trên R và đồ thị mặt dưới. Tìm quý giá thực của tham số m làm thế nào cho phương trình f(x) + m + 1 = 0 có 1 nghiệm duy nhất.
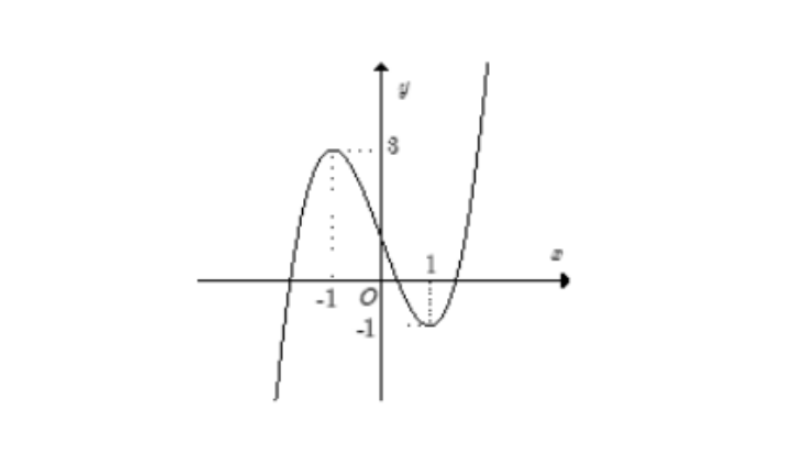
Hướng dẫn giải:

Dạng 5: Tiếp xúc giữa 2 con đường cong
Lý thuyếtĐường cong y = f(x) và y = g(x) tiếp xúc với nhau lúc hệ phương trình f(x) = g(x) với f’(x) = g’(x) gồm nghiệm và nghiệm là hoành độ tiếp điểm của 2 mặt đường cong đó.Nếu 2 đường cong tiếp xúc tại M(x0;y0), khi đó phương trình tiếp con đường tương giao thiết bị thị hàm số chung của 2 vật dụng thị y = g’(x0)(x – x0) + y0.Bài tậpCho 2 mặt đường cong y = x^3 – x + 1 với y = x^2 – 5/4x + 1. Chứng tỏ rằng 2 con đường cong tiếp xúc ở một điểm M như thế nào đó. Tìm tọa độ của tiếp điểm M cùng viết phương trình tiếp tuyến thông thường tương giao thứ thị hàm số.
Hướng dẫn giải:

Cách tìm chổ chính giữa đối xứng của trang bị thị hàm số
Lý thuyết rất đầy đủ về hàm con số giác
Hàm số với đồ thị hàm số y = a.x (a ± 0). Cách thức giải bài tập hay!
Tạm kết
Bài viết trên đây CMath đã thông tin đến bạn lý thuyết và bài xích tập áp dụng về tương giao vật thị hàm số. Đây là dạng toán khôn xiết thường chạm mặt và bao gồm nhiều phương pháp giải không giống nhau, chúng ta cần chú ý thật kỹ cùng làm bài xích tập nhằm ghi ghi nhớ các phương thức giải toán. Mong muốn các thông tin trên là hữu ích và giúp cho chính mình đạt được điểm tối đa trong số kỳ thi.
Bạn sẽ xem 20 trang mẫu của tài liệu "xemdiemthi.edu.vn Sử dụng phương thức đồ thị vào toán học để giải nhanh một vài bài tập Hoá học", để sở hữu tài liệu gốc về máy hãy click vào nút Download làm việc trên.File đính thêm kèm:

Nội dung text: xemdiemthi.edu.vn Sử dụng phương pháp đồ thị vào toán học để giải nhanh một số bài tập Hoá học
sở giáo dục và đào tạo và huấn luyện và giảng dạy Thanh hóa Trường trung học phổ thông hàm rồng sáng kiến kinh nghiệm "sử dụng cách thức đồ thị trong toán học để giải nhanh một trong những bài tập Hoá học" người viết: Nguyễn Thanh Hải Tổ: Hoá - Sinh - chuyên môn Năm học: 2006 - 2007Mục lục Trang A. Đặt vấn đề 3 B. Xử lý vấn đề 4 I. Phương pháp đồ thị 4 II. Những ví dụ 4 III. Phương pháp chung 9 IV. Tổ chức thực hiện 11 C. Tóm lại 12 Tài liệu xem thêm 1. Sách Hoá học tập Lớp 12 - NXB GD hà nội 2000. 2. Sách bài bác tập Hoá học Lớp 12 - NXB GD hà nội 2000. 3. Đề thi tuyển sinh vào những trường Đại học tập và cao đẳng NXB ĐHQG tp hà nội 1999-2001. 4. Đề thi lựa chọn học sinh giỏi môn Hóa học cấp Tỉnh, cấp giang sơn các năm. 2A. đặt vấn đề Trong tiếp thu kiến thức hoá học, việc giải bài xích tập tất cả một chân thành và ý nghĩa rất quan trọng. Ngoài câu hỏi rèn luyện kĩ năng vận dụng, đào sâu và không ngừng mở rộng kiến thức sẽ học một giải pháp sinh động; bài xích tập hoá học còn được dùng để làm ôn tập, tập luyện một số tài năng về hoá học. Trải qua giải bài xích tập, giúp học viên rèn luyện tính tích cực, trí thông minh, sáng tạo, bồi dưỡng hứng thú trong học tập. Vấn đề lựa chọn cách thức thích hợp để giải bài bác tập lại càng có ý nghĩa quan trọng hơn. Mỗi bài xích tập rất có thể có nhiều cách thức giải không giống nhau. Giả dụ biết lựa chọn phương pháp hợp lý, để giúp đỡ học sinh nắm rõ hơn bản chất của các hiện tượng hoá học. Qua quy trình giảng dạy, tu dưỡng học sinh tốt nhiều năm và việc tham khảo nhiều tài liệu, tôi sẽ tích luỹ được một số phương thức giải bài bác tập hoá học. Việc vận dụng cách thức đồ thị trong toán học nhằm giải nhanh một trong những bài tập hoá học đang tỏ ra có khá nhiều ưu điểm, nhất là khi những kỳ thi ngày này đã biến đổi sang cách thức TNKQ. Trong trường hòa hợp này, học sinh tiết kiệm được tương đối nhiều thời gian tính toán để có kết quả. Một trong những tác giả khác đã và đang đề cập đến giải pháp làm này trong một số trong những tài liệu tham khảo. Mặc dù nhiên, ở đó cũng mới chỉ dừng lại ở việc giải một số bài tập riêng biệt mà chưa có tính khái quát. Chính vì vậy, tôi viết đề tài này nhằm khái quát bài toán vận dụng phương pháp đồ thị trong toán học để giải một trong những bài tập hoá học. Trải qua đó tôi muốn giới thiệu với những thầy cô giáo và học sinh một trong những cách thức giải bài bác tập hoá học rất gồm hiệu quả. Vận dụng được phương pháp này để giúp cho quy trình giảng dạy với học tập môn hoá học tập được thuận lợi hơn hết sức nhiều, hối hả có công dụng để trả lời câu hỏi TNKQ. Đề tài được viết dựa trên cơ sở giải một số ví dụ nổi bật bằng hai phương pháp khác nhau. Trong số ấy có phương thức đồ thị trong toán học. Tổ chức đào tạo ở một lớp, review việc vận dụng phương thức này sau thời điểm đã được học tập tập. So sánh hiệu quả làm bài bác với một lớp không giống không được trình làng vận dụng cách thức đồ thị vào toán học tập học tập. Trên cơ sở kết quả thu được, nhận xét được ưu điểm và tổng quan thành phương pháp chung cho một vài dạng bài tập hoá học có thể giải bằng phương pháp này. 3B. Xử lý vấn đề I. Phương pháp đồ thị đại lý của phương pháp là việc thực hiện đồ thị vào toán học để giải một số hệ phương trình. Trong hoá học, một số dạng bài bác tập được giải dựa trên cơ sở ngôn từ của phương thức này. Đó là ngôi trường hợp nhưng trong thử nghiệm hoá học gồm hai quy trình lượng kết tủa tăng dần, sau đó giảm dần mang lại hết khi lượng chất làm phản ứng gồm dư. Hoàn toàn có thể vận dụng cách thức này trong hoá học ở những trường hợp đa phần sau: - Thổi khí CO2 vào dung dịch cất hiđroxit của sắt kẽm kim loại phân nhóm chủ yếu nhóm II. - Rót ung dung dung dịch kiềm cho dư vào dung dịch muối nhôm hoặc muối bột kẽm. - - Rót đàng hoàng dung dịch axit mang đến dư vào dung dịch muối bao gồm chứa anion AlO 2 2- hoặc Zn
O2 . Ta xem xét phương thức giải một vài bài tập dựa vào cơ sở kia thông qua một số ví dụ sau. II. Những ví dụ lấy ví dụ như 1: đến 10 lít (đktc) hỗn hợp A có N2 và CO2 sống đktc vào 2 lít hỗn hợp Ca(OH)2 0,02 M thì thu được 1 gam kết tủa. Tính % CO2 trong các thành phần hỗn hợp A theo thể tích (Sách Hoá học - Lớp 12 - NXB giáo dục và đào tạo Hà nội). Giải mã * phương thức tự luận: Phương trình hoá học của rất nhiều phản ứng lần lượt xẩy ra như sau: CO2 + Ca(OH)2 Ca
CO3 + H2O (1) CO2 + H2O + Ca
CO3 Ca(HCO3)2 (2) Ta có: Số mol Ca(OH)2 = 2. 0,02 = 0,04 (mol) Số mol Ca
CO3 = 1 : 100 = 0,01 (mol) Trường vừa lòng 1: Chỉ gồm phản ứng (1) Ca(OH)2 dư. Theo phương trình ta có: Số mol CO2 = Số mol Ca
CO3 = 0,01 (mol) = Số mol Ca(OH)2 0,01 22,4 Vậy, A gồm % CO2 = 100% 2,24% 10 Trường hòa hợp 2: Cả bội phản ứng (1) với (2) đều xẩy ra Ca(OH)2 hết. Theo phương trình (1): Số mol Ca
CO3 (1) = Số mol Ca(OH)2 = 0,04 (mol). Số mol Ca
CO3 (2) = 0,04 - 0,01 = 0,03 (mol). Theo phương trình (1) cùng (2): Số mol CO2 = 0,04 + 0,03 = 0,07 (mol) 0,07 22,4 Vậy, A có % CO2 = 100% 15,68% 10 * phương pháp đồ thị: dựa vào tỷ lệ phản bội ứng nghỉ ngơi phương trình (1) cùng (2) ta vẽ được đồ vật thị màn biểu diễn lượng kết tủa thu được theo lượng CO2 vẫn phản ứng như sau: Số mol Ca
CO3 0,04 0,01 0,01 0,04 0,07 0,08 Số mol CO2 nhờ vào đồ thị, trường hợp sau phản nghịch ứng thu được 1 gam kết tủa thì ta bao gồm ngay: Trường hợp 1: Số mol CO2 = 0,01 (mol). Trường đúng theo 2: Số mol CO2 = 0,07 (mol). Lấy ví dụ 2: Hoà tung 26,64 gam chất X là tinh thể muối hạt sunfat ngậm nước của kim loại M hoá trị n vào nước được dung dịch A. đến A tác dụng với dung dịch NH3 dư, lọc lấy kết tủa, nung đến trọng lượng không đổi thì nhận được 4,08 gam hóa học rắn B. Nếu đến A tính năng với dung dịch Ba
Cl2 dư thì thu được 27,96 gam kết tủa. A. Tìm phương pháp của X. 5b. Tính thể tích hỗn hợp Na
OH 0,2 M nên thêm vào A để thu được lượng kết tủa mập nhất, nhỏ tuổi nhất. C. Cho 250 ml hỗn hợp KOH tác dụng hết với A thì nhận được 2,34 gam kết tủa. Tính độ đậm đặc của hỗn hợp KOH. (Đề thi tuyển sinh - NXB Giáo dục thành phố hà nội - 1998). Lời giải a. Tác dụng tính toán cho ta phương pháp muối là: Al2(SO4)3.18H2O. Như vậy, hỗn hợp A có: 3+ 2 4,08 Số mol Al = 2. Số mol Al2O3 = 0,08 (mol). 102 * cách thức tự luận: Phương trình hoá học của các phản ứng lần lượt xảy ra như sau: 3+ - Al + 3 OH Al(OH)3 (1) - - Al(OH)3 + OH Al
O2 + 2 H2O (2) b. Để lượng kết tủa lớn nhất thì chỉ xẩy ra phản ứng (1). Theo phương trình: Số mol OH- = 3. Số mol Al3+ = 3. 0,08 = 0,24 (mol) Để lượng kết tủa nhỏ nhất thì xảy ra cả phản ứng (1) với (2). Theo phương trình: Số mol OH- = 4. Số mol Al3+ = 4. 0,08 = 0,32 (mol) Vậy, thể tích dung dịch Na
OH 0,2 M yêu cầu thêm vào A nhằm lượng kết tủa thu được lớn nhất, nhỏ nhất tương ứng là: V = 0,24 : 0,2 = 1,2 (lít) cùng V" = 0,32 : 0,2 = 1,6 (lít). C. Số mol kết tủa Al(OH)3 chiếm được là 2,34 : 78 = 0,03 (mol). Trường đúng theo 1: Chỉ bao gồm phản ứng (1) Al3+ dư. Theo phương trình ta có: - Số mol OH = 3. Số mol Al(OH)3 = 3. 0,03 = 0,09 (mol) 3+ Số mol Al (pư) = Số mol Al(OH)3 Theo phương trình (1): 3+ Số mol Al(OH)3 (1) = Số mol Al = 0,08 (mol). Số mol Al(OH)3 (2) = 0,08 - 0,03 = 0,05 (mol). Theo phương trình (1) với (2): Số mol OH- = 3. 0,08 + 0,05 = 0,29 (mol) 0,29 Vậy, nồng độ dung dịch KOH là:
OH thì thu được hỗn hợp A và 3,36 lít H2 (đktc). A. Tính m. B. Rót thong thả dung dịch HCl 0,2 M vào A thì thu được 5,46 gam kết tủa. Tính thể tích dung dịch HCl đang dùng. Giải mã a. Phương trình phản ứng: 72 Al + 2 H2O + 2 Na
OH 2 Na
Al
O2 + 3 H2 Theo phương trình: Số mol Al = 2/3. Số mol H2 = 0,1 (mol). M = 2,7 (gam). * phương thức tự luận: Phương trình hoá học của rất nhiều phản ứng lần lượt xẩy ra như sau: + - H + H2O + Al
O2 Al(OH)3 (1) + 3+ 3 H + Al(OH)3 Al + 3 H2O (2) b. Theo trả thiết: Số mol Al(OH)3 = 5,46 : 78 = 0,07 (mol) - Trường đúng theo 1: Chỉ có phản ứng (1) Al
O2 dư. Theo phương trình ta có: + Số mol H = Số mol Al(OH)3 = 0,07 (mol). - Số mol Al
O2 (pư) = Số mol Al(OH)3 phụ thuộc tỷ lệ phản nghịch ứng nghỉ ngơi phương trình (1) cùng (2) ta vẽ được trang bị thị màn biểu diễn lượng kết tủa chiếm được theo lượng H+ đang phản ứng như trên. B. Ví như sau bội phản ứng chiếm được 5,46 gam kết tủa thì: Trường hợp 1: Số mol H+ = 0,07 (mol). Trường hợp 2: Số mol H+ = 0,19 (mol). III. Phương pháp chung Qua việc giải những bài tập nghỉ ngơi trên bởi hai phương pháp khác nhau ta thừa nhận thấy: - hoàn toàn có thể giải một số trong những bài tập hoá học tập theo phương pháp đồ thị một cách nhanh chóng mà không xẩy ra bỏ sót nghiệm. - những bài tập hoá học giải được theo cách thức này gồm hai loại chủ yếu sau: 1. Tính lượng hóa học đã bội nghịch ứng khớp ứng với lượng kết tủa thu được. 2. Tìm đk để khối lượng kết tủa thu được phệ nhất, nhỏ dại nhất. Dạng 1: Thổi ung dung khí CO2 cho dư vào dung dịch cất a mol Ca(OH)2 hoặc Ba(OH)2. Sau phản ứng chiếm được b mol kết tủa. Số mol kết tủa a b x a y 2a Số mol CO2 Số mol CO2 sẽ phản ứng là: x = b (mol) y = 2a - b (mol). Dạng 2: Rót thư thả dung dịch kiềm đến dư vào dung dịch đựng a mol muối hạt Al3+ hoặc Zn2+. Sau phản ứng nhận được b mol kết tủa. * Số mol OH- đã phản ứng là: x = 3b (mol) y = 4a - b (mol). Số mol Al(OH)3 9a b Số mol OH- x 3a y 4a Số mol Zn(OH)2 a b Số mol OH- x 2a y 4a * Số mol OH- vẫn phản ứng là: x = 2b (mol) y = 4a - 2b (mol). Dạng 3: Rót thủng thẳng dung dịch axit cho dư vào dung dịch đựng a mol muối bột - 2- Al
O2 hoặc Zn
O2 . Sau phản bội ứng nhận được b mol kết tủa. Số mol Al(OH)3 a b Số mol H+ x a y 4a * Số mol OH- vẫn phản ứng là: x = b (mol) y = 4a - 3b (mol). Số mol Zn(OH)2 a b Số mol H+ x 2a y 4a * Số mol H+ vẫn phản ứng là: x = 2b (mol) y = 4a - 2b (mol). IV. Tổ chức tiến hành 10








