Script has been disabled on your browser, please enable JS khổng lồ make this app work.
Bạn đang xem: Phương pháp học xác suất
Xác suất với thống kê được coi là một trong số những môn học hóc búa nhất đối với học sinh, sinh viên. Bởi vì vậy, phương thức họcmoon này sao cho hiệu quả luôn là vấn đề mà rất đa số chúng ta quan tâm. Nội dung bài viết dưới đây sẽ ra mắt cho chúng ta 5 mẹo học tỷ lệ thống kê lấy điểm cao. Nếu như bạn đang còn loay hoay cùng với môn học tập này thì đừng bỏ dở những mẹo sau đây nhé!
1. Đọc giáo trình trước lúc lên lớp
Bởi đây là một môn khá cực nhọc cho sinh viên, việc làm rõ nội dung bài học hôm nay như nào, cùng để đuổi theo kịp với tốc độ giảng của giảng viên, ta nên đọc kĩ trước lúc học.Ta nên take lưu ý nội dung chính lên quyển sổ hay là một app note cho việc tiện gọi lại cùng thi.Mình recommend một quyển giáo trình rất hữu dụng cho sinh viên, các chúng ta cũng có thể tham khảo tại đây
2. Hiểu cùng nhớ những khái niệm về tỷ lệ thống kê
Các khái niệm/thuật ngữ liên quan đếnProbability and Statistics– tỷ lệ và thống kê thường khá khó khăn nhưng hiểu nó đó là bước đầu tiên phải làm cho để bạn có thể đạt điểm cao. Tỷ lệ và thống kê gồm có khái niệm rất giản đơn nhầm lẫn với nhau buộc phải nếu đọc từng tư tưởng thì mới rất có thể phân biệt được. Nếu thiếu hiểu biết nhiều và lưu giữ rõ từng có mang thì bạn sẽ gặp khá nhiều khó khăn trong câu hỏi hiểu được thực chất của mọi vấn đề phức hợp sau này.
Sau khi đã làm rõ được các khái niệm về phần trăm thống kêthì bài toán nhớ chúng không còn là điều khó khăn nữa. Cần hiểu rằng việc nhớ sống đây không hẳn là chỉ nhớ nội dung của quan niệm mà cần nhớ được thực chất của nó. Vấn đề nhớ những khái niệm giúp bọn họ phân biệt cấp tốc và công dụng nhất, ví dụ khác nhau chỉnh hợp cùng tổ hợp.
3. Rứa vững những kiến thức về phần trăm thông kê
Các loài kiến thức định hướng về xác suất – thống kê cũng đặc biệt tương trường đoản cú như những khái niệm vềProbability và Statistics. Để rất có thể thực hành thì tất yêu không chũm lý thuyết.Những bài học kinh nghiệm về triết lý thường bị bỏ qua do một số trong những bạn cho rằng nó dễ dàng và đơn giản nên không yêu cầu chú trọng. Nhưng lại đây chính là cơ sở mang lại những bài học kinh nghiệm sau.
Để thay vững những kiến thức về lý thuyết xác suất – thống kê, chúng ta nên nỗ lực tìm cách liên hệ giữa bài xích tập, bài xích học, công thức với thực tế. Điều này khiến cho bạn vừa nắm vững được mọi kiến thức kim chỉ nan trên sách vở, vừa vận dụng vào thực tiễn của môn học một giải pháp hiệu quả.
4. Học từ trên đầu và triệu tập cao độ
Thế nào là học từ đầu? bọn họ gặp không ít trường hợp chúng ta sinh viên khi học môn xác suất thống kê tuy nhiên lại không học tập từ đầu, vì một lí vị nào đó chúng ta học từ bài bác thứ ba, thứ tư hay từ giữa kì học trở đi điều này là sự việc thiệt thòi lớn cho những bạn.Những bài học trước tiên của bất kể môn học nào cũng đều rất đặc biệt quan trọng bởi sẽ là nền tảng, cửa hàng để chúng ta học các bài tiếp theo một các logic.
Việc vứt qua các bài học trước tiên là các bạn đã bỏ qua mất nền móng mang đến mình, trong khi những người khác đã tích lũy kiến thức và kỹ năng mới thì bản thân vẫn loay hoay để cố hiểu những gì mình không học. Bí quyết học phần trăm thống kê này vô cùng quan trọng.
5. Lựa chọn cách thức học tập phù hợp
Mỗi người đều phải sở hữu một “phong bí quyết học tập” đặc trưng hiệu quả nhất với mình.Hãy tìm ra cách thức phù phù hợp nhất cho bạn và tận dụng tối đa cách học đó. Bạn sẽ được chủ động lựa chọn cách thức học lúc ở nhà, nhưng bạn cũng có thể đề xuất giáo viên kiểm soát và điều chỉnh cách giảng bài đa dạng mẫu mã và cân xứng hơn với phong thái học của mỗi học sinh.
Ví dụ, chúng ta có thấy mình dễ dàng nhớ những biểu vật dụng hay tranh hình ảnh không? rất có thể bạn là tín đồ học qua thị giác và nên thực hiện nhiều tranh hình ảnh để học. Bạn có thể tự vẽ biểu đồ nhằm ghi nhớ những phần trong bài bác nói.Bạn thấy mình tiếp thu dễ dàng hơn lúc vừa học vừa nghe nhạc khe khẽ, hoặc chúng ta không nhớ ngôn từ viết nằm trong bảng nhưng hoàn toàn có thể “nghe thấy” rất nhiều điều thầy cô nói, như thể họ vẫn giảng bài trong chống bạn. Điều này có nghĩa chúng ta là tín đồ học qua thính giác, có nghĩa là bạn học hiệu quả hơn với âm thanh. Bạn cũng có thể thu âm bài bác giảng của thầy cô để nghe lại lúc làm bài tập tuyệt ôn tập.6. Đọc những tài liệu tham khảo
Một tuyệt kỹ nữa để có thể dễ dàng quá qua phần trăm và thống kê chính là đọc những tài liệu tham khảo. Khi đọc nhiều, bạn sẽ tiếp thu thêm được phần đông kiến thức nhiều mẫu mã khác ngoài các tài liệu được giáo viên cung cấp. Những thông tin được bổ sung cập nhật thêm chắc chắn sẽ góp bạn tiện lợi hơn trong việc làm bài bác tập. Xung quanh ra,probability and statisticslà nghành nghề dịch vụ được ứng dụng rất nhiều trong cuộc sống thường ngày hiện nay, từ bỏ engineering mang đến business, economy tốt những nghành đời thường nhất. Khi chúng ta xử lý dữ liệu để lấy ra quyết định cũng chính là bạn đang cần sử dụng đếnprobability và statistics.Chính vì chưng vậy việc đọc các tài liệu tham khảo không chỉ là cách làm bài tập phần trăm thống kê hơn nữa là cách để bạn có thêm các kinh nghiệm thực tiễn rất hữu ích cho mình trong việc giải quyết và xử lý những vụ việc trong cuộc sống.
Các tài liệu mình recommend:
7. Ôn tập trước kì thi sớm
Một trong số những cách hữu hiệu nhất nhằm đạt thành tích cao trong các bài khám nghiệm là ôn tập và sẵn sàng càng mau chóng càng tốt. Tuyệt vời không để chứng trạng một ngày trước lúc thi mới ban đầu ôn tập. Bài xích thi càng cực nhọc thì các bạn càng cần ôn luyện sớm, cực tốt là 2 hoặc 3 tuần trước lúc kiểm tra.
-----------------------
(*) Follow Facebook
Top
Tip - share Bí cấp bách Học Tập, Nghề Nghiệp, cuộc sống đời thường Thú Vịđể đọc các bài viết khác và cập nhật thông tin hữu dụng hằng ngày.
(**) đổi thay Tình nguyện viên, Thực tập sinh Part-time tại Top
Tip để chia sẻ và đóng góp học thức cho cùng đồngtại đây
Chọn mẫu là ngôn từ rất quan trọng trong nghiên cứu vì tương quan trực kế tiếp tính đại diện cho nhóm. Chủng loại mang tính đại diện cho nhóm càng tốt thì số liệu điều tra càng có mức giá trị với độ tin yêu của phân tích càng cao. Nội dung bài viết này đang giới thiệu chi tiết về các cách thức chọn mẫu tỷ lệ và ưu, điểm yếu kém của từng giải pháp chọn mẫu.
Chọn mẫu mã ngẫu nhiên đơn giản (simple random sampling)
Là kỹ thuật lựa chọn mẫu, trong đó, tất cả cá thể vào quần thể bao gồm cùng thời cơ (cùng xác suất) nhằm được lựa chọn vào mẫu.
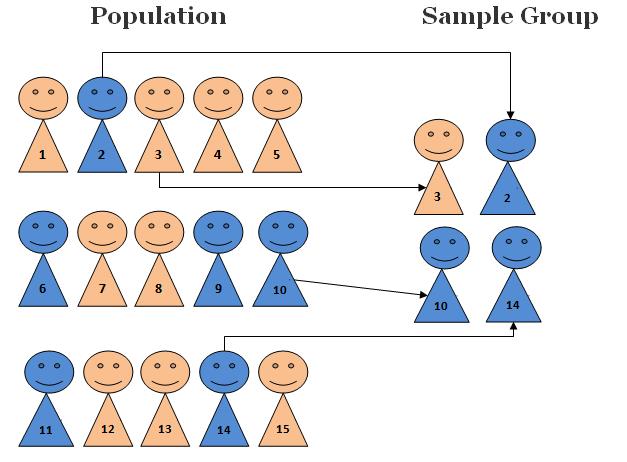
Ví dụ: khi mong mỏi chọn 300 người trong các 3.000 sinh viên tại trường đh X thì mỗi sinh viên có phần trăm là 10% được lựa chọn vào mẫu. Công việc thực hiện như sau:
- cách 1: Lập khung mẫu mã chứa tất cả sinh viên của trường đh X.
- bước 2: lựa chọn mẫu bất chợt bằng những cách thức: tung đồng xu, tung xúc xắc, bốc thăm, bảng số bỗng nhiên hoặc thực hiện phần mềm laptop như vòng quay,… để chọn.
Chọn chủng loại ngẫu nhiên khối hệ thống (systematic random sampling)
Theo phương pháp chọn mẫu tình cờ hệ thống, vớ cả đối tượng trong toàn diện và tổng thể được liệt kê theo đồ vật tự định trước. Tiếp đến tùy vào quy mô mẫu mã và toàn diện mà quyết định khoảng cách các mẫu.
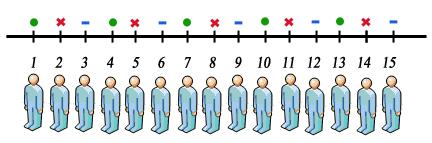
Cách lựa chọn mẫu: chia N (tổng thể) thành n nhóm, trong các số đó mỗi nhóm tất cả k đối tượng. Sau đó, khoảng chừng lấy mẫu k = N/n được áp dụng để tạo nên thành team mẫu.
Xem thêm: Khám Phá 14 Địa Điểm Vui Chơi Gần Sài Gòn Cho Cuối Tuần Năng Động
Ví dụ: yêu cầu đưa ra là buộc phải chọn 5 khách hàng từ nhóm trăng tròn khách hàng. Cách thức thực hiện như sau:
- Tính khoảng cách mẫu: k = 20/5 = 4
- Chọn hốt nhiên một quý giá r: 1 =Khách hàng đồ vật nhất: số đồ vật tự là 3Khách hàng máy hai: số thứ tự là 3 + 1(4) = 7Khách hàng trang bị ba: số máy tự là 3 + 2(4) = 11Khách hàng thứ tư: số trang bị tự là 3 + 3(4) = 15Khách hàng vật dụng năm: số thứ tự là 3 + 4(4) = 19
Chọn mẫu ngẫu nhiên phân tầng (stratified random sampling)
Là kỹ thuật chọn mẫu được tiến hành bởi việc chia toàn diện thành những nhóm riêng lẻ được call là tầng (ví dụ: giới tính, độ tuổi, thu nhập, chuyên môn học vấn,…). Đặc điểm của chọn mẫu phong cách này là tiêu chí nghiên cứu và phân tích trong từng tầng tương đối đồng nhất, còn giữa những tầng có sự khác biệt. Sau khoản thời gian đã phân tầng hoàn thành ta vẫn có thể áp dụng cách chọn chủng loại ngẫu nhiên dễ dàng hoặc ngẫu nhiên khối hệ thống để chọn đối tượng người dùng của từng tầng vào nghiên cứu.
Hình 3 minh họa một ví dụ đối chọi giản, trong những số đó nhóm mẫu gồm 10 đáp viên được chọn bằng cách chia thành những nhóm (tầng) phái mạnh và bạn nữ để thay mặt của cả hai giới được đồng hầu như trong team mẫu.

Chọn mẫu tự nhiên cụm (cluster sampling)
Là kỹ thuật chọn mẫu trong số đó việc chắt lọc ngẫu nhiên các nhóm thành viên (ví dụ trong cùng làng, xã, ngôi trường học, khoa phòng, dịch viện,…) từ rất nhiều cụm trong một quần thể nghiên cứu. Vào trường đúng theo này, đơn vị chức năng mẫu là những cụm chứ chưa hẳn là những cá thể. Cách thực hiện:
Bước 1: xác minh các nhiều thích hợp.
Bước 2: Lập danh sách tất cả các cụm, chọn ngẫu nhiên một số trong những cụm vào mẫu. Tất cả hai biện pháp chọn mẫu theo ý tưởng của tín đồ nghiên cứu:
Cách 1: tất cả các cá thể trong các cụm đã lựa chọn vào nghiên cứu.Cách 2: Liệt kê danh sách các cá thể trong số cụm đang chọn, kế tiếp áp dụng bí quyết chọn mẫu mã ngẫu nhiên solo hoặc ngẫu nhiên khối hệ thống trong mỗi cụm để chọn các cá thể vào mẫu.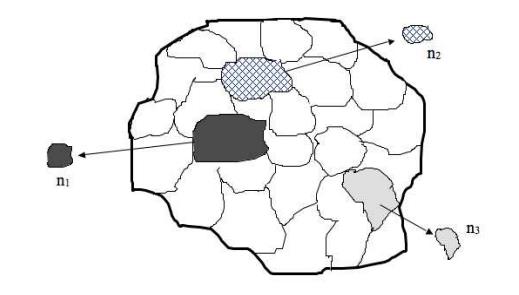
Chọn mẫu các bậc (Multistage sampling)
Chọn mẫu các bậc là dạng đem mẫu kết hợp nhiều phương pháp chọn chủng loại với nhau. Lựa chọn mẫu các bậc gồm tính vận dụng cao, cân xứng trong điều kiện các nghiên cứu và phân tích với tổng thể phức tạp.
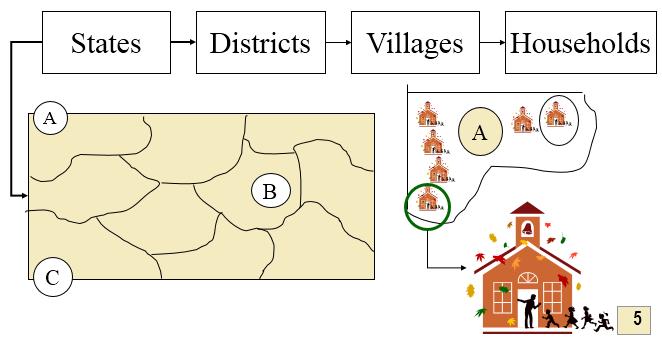
Ví dụ: để nghiên cứu và phân tích 1.000 hộ nông dân trồng lúa trong tỉnh X, người ta đã chắt lọc như sau:
Chọn 5 huyện trong tỉnh XTrong từng huyện sẽ chọn, lựa chọn 4 xãTại từng xã sẽ chọn, lựa chọn 5 ấp
Với từng ấp, lựa chọn 10 hộ nông dân
Sau đó, tiến hành nghiên cứu dựa trên số mẫu mã thu được.
Ưu nhược điểm của những cách chọn mẫu xác suất
| Phương pháp chọn mẫu | Ưu điểm | Nhược điểm |
Ngẫu nhiên đối chọi giản | Dễ thực hiện, tính khả quan cao. Có thể đan xen vào tất cả các kỹ thuật lựa chọn mẫu tỷ lệ phức tạp khác. | Cần phải có một danh sách của các đơn vị mẫu. Không dùng được mang đến mẫu khủng hoặc mẫu mã dao động. Mẫu được chọn có thể phân tán khó thu thập. Có tài năng bỏ sót vài team trong tổng thể. |
Chọn mẫu mã hệ thống | Nhanh, dễ thực hiện. Độ chính xác cao, chọn đối tượng người sử dụng theo mục tiêu điều tra. Tính thay mặt đại diện cao hơn. | Có thể bị trùng lặp, dẫn đến mẫu thiếu thốn tính đại diện |
Chọn mẫu mã phân tầng | Độ đúng chuẩn cao. Tính thay mặt đại diện cao hơn cùng dễ làm chủ mẫu ngẫu nhiên đối chọi giản. | Cần tùy chỉnh thiết lập khung mẫu mang lại từng tầng. Điều này thường xuyên khó tiến hành trong thực tế. |
Chọn chủng loại theo cụm | Áp dụng mang lại phạm vi rộng lớn lớn, độ phân tán cao. Dễ lựa chọn và chi tiêu rẻ hơn. | Tổng thể yêu cầu lớn. Nếu thuộc cỡ chủng loại tính đại diện hoặc tính chính xác thấp hơn mẫu ngẫu nhiên đối kháng giản. |
Chọn mẫu những bậc | Hiệu quả trong việc thu thập dữ liệu sơ cấp. Hiệu quả về chi tiêu và thời gian. Mức độ hoạt bát cao. | Mức độ khinh suất cao. Công dụng nghiên cứu không khi nào có thể đại diện 100%. Sự hiện hữu của tin tức cấp team là bắt buộc. |
Lưu ý:
Dữ liệu sơ cấp: là đa số dữ liệu không tồn tại sẵn, được người nghiên cứu thu thập.Dữ liệu thức cấp: là tài liệu được tích lũy dựa trên những tư liệu bao gồm sẵnMinh Thư
----------------------------------------
Chọn chủng loại trong phân tích - Phần 1: một vài khái niệm và phương thức chọn mẫu
Chọn mẫu trong phân tích - Phần 3: cách thức chọn mẫu mã phi xác xuất (non-probability sampling)
Chọn chủng loại trong phân tích - Phần 4: vận dụng các phương thức chọn mẫu
----------------------------------------
Tài liệu tham khảo:
<1> Hoàng Văn Minh, giữ Ngọc Hoạt. Phương pháp chọn chủng loại và tính toán cỡ mẫu mã trong nghiên cứu và phân tích khoa học sức khỏe. Http://cphs.huph.edu.vn/uploads/tintuc/2020/Phuongphapchonmauvatinhtoancomau.pdf <2> John Dudovskiy. Simple Random Sampling. Https://research-methodology.net/sampling-in-primary-data-collection/random-sampling/
---------------------------------------------------------------------------------------------------
QUÝ ANH/CHỊ CẦN HỖ TRỢ XỬ LÝ, PHÂN TÍCH DỮ LIỆU VUI LÒNG GỬI THÔNG TIN QUA form DƯỚI ĐÂYCHÚNG TÔI SẼ LIÊN HỆ VÀ PHÚC ĐÁP trong THỜI GIAN SỚM NHẤT







